The first calculator I devised was meant to take the place of the map view in IVA-only challenges. as such, it can only be used to plan rudimentarally. But if you ever wanted to know how it worked and how you can do all the equations by yourself, here's how. Note: I originally put this on a single page with all the rest of my knowledge on orbital mechanics, but I felt it was better to seperate them all. As such, this may look a bit odd.
If you have played Kerbal Space Program and gone into the capsules, you'll realise that they're pretty bare-bones. An altimeter, a nav-ball, a rate of climb/decent gauge, a speed indicator, and maybe a radar altimeter if you're lucky.

But what if I told you that, using these instruments and some basic information about the parent body, you can determine both your orbit and where you are in it?
To prepare, you're going to have to get a way to accurately read these gauges. I use Kerbal Engineer Redux (Which can do all the equations I am about to show you for you, but can also display useful info. I use it for the latter.). You're going to your speed indicatior (set to orbit mode, because surface or target mode will give you wrong answers), rate of climb/decent indicatior, and your altimeter, or digital equivalents of such if you cannot read the stock gauges well.
You're also going to need how wide your parent body is (its radius, denoted by c), and it's specific Gravitational Parameter. What is that? Well, Gravitational Parameter (Or k, as I will refer to it as) is the result when the graviational constant G is multiplied by the parent body's mass M. These measurements are body specific, so figure out what they all are before going to any planet.
Once you have your k, take your vertical velocity v, your total orbital velocity t, and your ASL altitude d. This will help us form a vector: We first get horizontal velocity h:
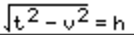
Then we add our ASL altitude to the altitude of the planet to get radius, or how far we are from the center of the planet:
Insert image of c+d=r(Admittedly, this last one does not require an entire image, but it's good to keep consistent)
Now, we have to do some calculating to get a. Admittedly, it's really simple to get a with the right variables: Take apoapsis radius, add periapsis radius, then divide by 2. However, since we don't actually know Apoapsis and Periapsis yet, we'll have to do things the hard way. The equation we use for this is:
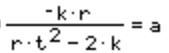
The value you end up with tells you what type of orbit you have. A positive answer means you have gotten into a bounded Elliptical or Circular orbit. A negative answer tells you you have an unbounded Hyperbolic orbit. And if you somehow get an answer with the words 'divide by zero', pat yourself on the back and stop calculating. You have entered a parabolic orbit, with an undefined periapsis and an eccentricity of 1. It doesn't matter what you put in - these are the values for all parabolic orbits.
if you didn't get an answer divided by zero, you can now calculate eccentricity, e. This is given by:
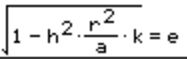
Which requires that h we calculated at the beginning. If you get an answer of less than 1, it is a bounded orbit (an Ellipse or a circle). If it is more than 1, it is unbounded (a hyperbola). If it is exactly 1… what are you still doing here? I told you to stop calculating!
Let's calculate Period p next. It only will work if a is positive and e is less than 1, due to the fact that only bounded orbits are periodic (IE, only circles and ellipses repeat in their motions.) If you put in meters, the answer it gives will be in seconds. The equation for Period is:
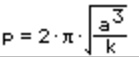
finally, you can calculate your True Anomaly. The equation we use is simply the Polar ellipse equation, solved for θ. Why do I have two equations here?
Well, to get θ by itself, you have to invert a cosine. Now, (cos-1, or arccos) can only give one answer, but cosine can give two. That means we need two equations, a positive and a negative, and we need to choose. This is why I expressed my version of true anomaly as being between -180 and 180: This way, you can just use whether you've passed Apoapsis or not as the decider. Since passing Apoapsis means you are falling towards the planet, and going to Apoapsis means you are moving away, just check your rate of climb indicatior to decide which equation.
This is the equation:
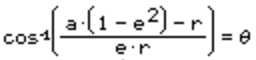
And if your Vertical velocity is negative, you're going to want to invert it.
If you want to calculate some more parts of your orbit, you can calculate Periapsis n (and, if your eccentricity is less than 1, your Apoapsis f) with these two equations:
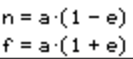
And then you can calculate Speed At Apsides(q for S@Pe,s for S@Ap) with these equations:
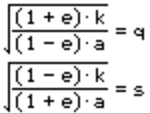
And that's all I know to do as of now (20171114133400)
Back to home